This time I swear it's the last part, Promise!

In Part 1, I showed you how to perform a Fourier transform with Python and how to analyze the spectrum AND — I’ll never shut up about it — the phase.

So, I fulfilled my contract! I take the check — assuming bank checks are still a thing — and ride off into the sunset?

This time we start from the assumption that it’s the underlying trends that drive the stock market signal. In other words, it’s the long cycles that matter when trying to figure out if the price is about to crash like Tesla stock after every random tweet from its CEO, or explode like Bitcoin whenever your Uber driver tells you it’s the next bull run, "to the moon, bro, 100k easy."

Anyway, if I’ve done my job right, talking about "long cycle detection" should make you think of:

1. the long wash cycles on your washing machine — let's be honest, two articles aren’t enough to rewire your brain just yet,
2. Fourier theory and cycle analysis: You should instinctively link "long cycle" with low frequency.Thus, since we’ll be focusing on low frequencies, it means chopping off the high frequencies.
   

You should also note the flip side of our assumption: we don’t want short cycles.
The market view behind this is that short cycles represent volatile, unpredictable changes — in short, noise.
Keep in mind that, in this specific framework, we’ll consider high frequencies as noise to be removed, leaving us with the famous de-noised signal — or as quants like to fantasize, the holy grail: the "pure" signal, stripped of all randomness and chaos… basically the quant version of Santa Claus. 

Frequency-Based Processing

I believe that if you’re going to do filtering, it's absolutely crucial to actually know a bit about filtering — just common sense! 😑

The first type of filter I’ll introduce you to is the perfect filter: it zeroes out the amplitude of every frequency above a defined cutoff. Physically, it’s impossible to build because it causes nasty Gibbs artifacts, but because we're simulating things on a computer, it ends up looking way cleaner.

It's the theoretical perfect filter, and it's always smart to start with it, because you know it’ll wipe out all the high frequencies completely. After an inverse FFT, you should see a much smoother signal (and the lower your cutoff frequency, the smoother it'll get) — a bit like an EMA where you crank the smoothing period way up.However, like anything that's too black-and-white, this method falls apart in real-world cases. 

Here’s a quick analogy:
Saying “The English are losers” is like using a too-aggressive filter that wipes out all the rich harmonics.
What you should say is:“The English have a centuries-old tradition of getting thrashed by France, lovingly preserved from Hastings to Waterloo, with pit stops at Poitiers and Castillon.”
Now you're capturing those juicy subtleties — the little historical collapses, the subtle shifts, the weak signals a brain-dead filter would toss away. And that, my friends, is the beauty of high frequencies — with a salty kiss tossed across the victorious side of the Manche, aka the "English Channel" 😘.

Thus, in real-life scenarios, you need filters that are a bit less brutish and a bit more nuanced. To handle this, you’ve got two big options: IIR or FIR filters. To help me choose, I usually ask myself one simple question: 

Do I want my signal to stay stable ?

If yes, I need a filter that never blows up and keeps the phase profile nice and clean. In that case, FIR is the way to go.
If I want a filter that adapts based on previous outputs (and am willing to gamble a bit on possible divergence), then I’ll go for an IIR.

Next step: I hit the supermarket and pick whatever looks tastiest off the shelf:

• FIR: moving average, rectangular window, Hamming window, Hann window, equiripple FIR, etc.
• IIR: EMA, Butterworth, Chebyshev (Type 1 and 2), Bessel, elliptic...

And here — brain neuron activation — yes! A moving average is just an FIR filter, and an EMA is an IIR filter.
See, a moving average only considers a sliding window of points, whereas an EMA also takes previous results into account  — it’s sneaky and retroactive, like your browser history you thought you deleted.😏

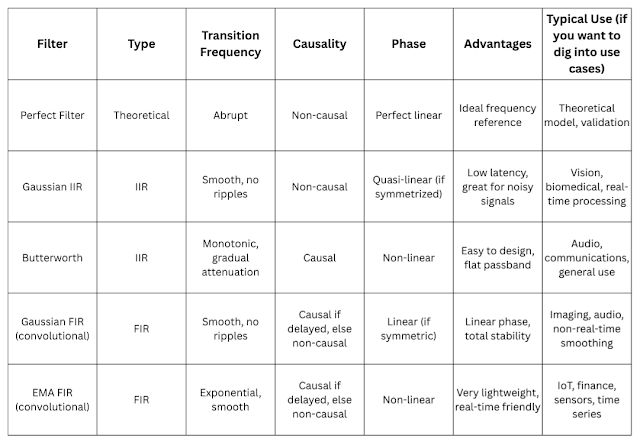
Here’s a comparison table with my favorite filters — who's down for a tier list?

Causality in a digital filter means its output at a given time only depends on past and present inputs, never future ones. In other words, a causal filter can't "see" into the future: it can only use the data available up to the current instant.
Imagine a centered convolution filter using values [t-2, t-1, t, t+1, t+2]—then it's non-causal because to calculate the value at t, you have to cheat and peek into the future. However, after processing, you get a super-smooth curve that beautifully takes everything into account... but it’s not usable directly in trading because of look-ahead bias and a fat risk of overfitting.
In our case, though, we stick to the same method as before:

1. import a snapshot of the price
2. fft
3. filtering
4. prediction

Thus, using a non-causal filter isn’t catastrophic since we’re already working on a frozen snapshot at time t.
However, beware: this kind of filter might model our curve too well, and end up overfitting the signal. That’s kind of what we want for analysis and filtering purposes—but it also means you might start seeing beautiful trends that are as real as a Tinder bio.
That’s just my intuition for now, I haven’t yet proved it systematically!

If you don’t feel like playing chicken on the highway—where, you know, everything hits you at 150 mph—I recommend using a causal filter ([t-2, t-1, t] to calculate t), but keep in mind you’ll have to deal with a time lag due to filtering and probably some phase correction too.
We would therefore generally choose the causal Gaussian filter (FIR) because its phase is linear and much easier to realign.

Phew! I’ll stop the filtering theory brain dump here... now onto actual results.😁

Frequency Filtering

First, we’re going to do some perfect frequency filtering. For that, you pick a cutoff frequency — basically the frequency beyond which the intensity gets murdered (i.e., set to zero). Then you just zero out everything that comes after. Simple enough, right? Here's the code:

# Suppose x is your original DETRENDED signal
# n: number of samples, dt: sampling interval
fft_coeffs = np.fft.fft(x)
freqs = np.fft.fftfreq(n, d=dt)

# Filtering: keep frequencies < cutoff
cutoff = 1/50
fft_coeffs[np.abs(freqs) > cutoff] = 0

And honestly? It’s pretty damn good!🤩

Now, I’m going to jump straight to the part where I show you the function that handles the predictions. You've survived 2 articles and 1 random rant, so I’ll spare you any more pain. Here it is:

def fourier_extrapolation(x, n_predict, fs, cutoff=None):
    """
    Extrapolates the signal x by n_predict additional points using a Fourier series decomposition.
    Parameters:
        x         : numpy array containing the original DETRENDED signal.
        n_predict : number of points to predict.
        fs        : sampling frequency (e.g., 1/7).
        cutoff    : cutoff frequency (in Hz) for filtering; if None, no filtering.
    Returns:
        Extrapolated signal of size len(x) + n_predict.
    """
    n = x.size
    dt = 1 / fs  # Time interval (for fs=1/7, dt=7)

    # Compute the FFT
    fft_coeffs = np.fft.fft(x)
    
    # Low-pass filtering: eliminate frequencies higher than the cutoff
    if cutoff is not None:
        freqs = np.fft.fftfreq(n, d=dt)
        fft_coeffs[np.abs(freqs) > cutoff] = 0
        
    # Create an extended time vector (considering the time interval dt)
    t_extended = np.arange(0, n + n_predict) * dt
    # Reconstruct the signal using the Fourier series
    result = fft_coeffs[0].real / n * np.ones_like(t_extended)
    
    # Reconstruct for positive frequencies
    for i in range(1, n // 2 + 1):
        amplitude = 2 * np.abs(fft_coeffs[i]) / n
        phase = np.angle(fft_coeffs[i])
        result += amplitude * np.cos(2 * np.pi * i * t_extended / (n * dt) + phase)

    # If n is even, the Nyquist component should not be doubled
    if n % 2 == 0:
        nyquist = n // 2
        result += (np.abs(fft_coeffs[nyquist]) / n) * np.cos(2 * np.pi * nyquist * t_extended / (n * dt) + np.angle(fft_coeffs[nyquist]))
    return result

For those who followed the last article, this function will feel totally natural. The only real difference is handling whether the number of points in the signal is even or odd. Basically, when reconstructing the signal, I use the symmetry of the spectrum to pair up a positive frequency with its negative twin, summing them with a factor of 2/n. But if the signal length is even, there's a lone ranger frequency hanging around (the Nyquist frequency), so I deal with it separately with just a 1/n coefficient.

If the number of points is odd? No Nyquist orphan — simple.

This frequency is called the Nyquist frequency because it’s the max frequency you can actually spot without your signal turning into a Picasso painting (aliasing, ever heard of it?). It comes straight from the golden rule: you need to sample at least twice as fast as your highest frequency. If you forgot that, no worries — just pretend you knew and nod dramatically.😒

Here are the results for fs = 1/7, cutoff = 1/100, and n_predict = 30:

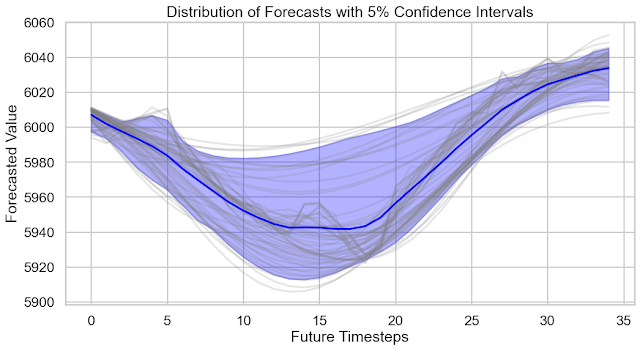
As before, we now build the distribution of our forecasts and display it:

denominators = np.arange(10, 300, 5)  # Range of denominators to test for cutoff frequency

# Compute all cutoff frequencies
cutoffs = 1 / denominators

# Perform Fourier extrapolation for each cutoff taking only the forecast
forecastm = np.array([
    fourier_extrapolation(x, n_predict, fs, cutoff)[-n_predict:]
    for cutoff in cutoffs
])

And guess what? We end up with a forecast space that's coherent across the different cutoffs. That’s pretty damn encouraging too.

Always pushing it further?

I hyped up my favorite filters at the start of this ride, no way I was gonna ghost them now — they'd haunt me in my sleep and honestly, I’ve got enough demons already.
Here’s the lineup I’m picking:

• Gaussian filter: an IIR that minimizes group delay — classy and efficient.
• Butterworth filter: to showcase a good ol’ classic IIR filtering case.
• Convolutional filter with a Gaussian kernel: FIR style, to really flex the difference between a Gaussian FIR and a Gaussian IIR. One of the best FIR filters you can throw into the ring — absolute basics, no excuses.
• Convolutional filter with an EMA kernel: in my opinion, one of the best FIR options out there when you’re messing with finance data and nonlinearities are throwing tantrums all over the place.

Alright, let’s hit it like a machine gun using fs = 1/7, cutoff = 1/100, and n_predict = 30 :
For the Gaussian IIR filter, here’s what I get:

For the Butterworth IIR filter with order 4:

For the Gaussian convolutional FIR filter:

And finally for the EMA convolutional FIR filter:

To make Fourier-based predictions even more bulletproof, you could also combine the forecasts (using again probability maps for each method) — not necessarily to make them truer (although it won’t hurt), but mainly to beef up the robustness of the whole process. Because honestly, if one filter goes batshit crazy, the other four are there to slap it back into reality before it tanks your decision-making. 

It's like your buddy, drunk at 3 AM, firing off texts to his ex — and just as you think he's about to make a huge mistake, the squad swoops in like a SWAT team, grabbing the phone and telling him to sleep it off before he burns any bridges.😉

Final Conclusion

Here’s a quick recap of the method developed in the article:

1. Import the data and detrend the signal
2. Use numpy to perform an FFT and create a frequency axis (here)
3.  Do I want to preserve the stability of my signal?
1. Yes: FIR, filters with bounded windows, like convolutions
2. No: IIR, all the rest of the filters
4. Filter the signal and reconstruct it to double-check everything
5. Forecasting and turning the forecast space into probabilities

Phew, finally tackled a big boy topic.
Hope you had a blast — 'cause writing this was a whole other beast!
Just kidding. Actually, reviewing all my courses and applying them in practice really helped hammer the knowledge deeper into my brain.
That said, feeling confident doesn't mean I'm suddenly Jesus of Signal Processing! If you spot any mistake, you better call me out in the comments — I’ll be there ready to brawl.🥊
By the way, let me know if you want the code I used for the predictions or whatever else!

No clue yet what the next topic will be, but I’m gonna keep it lighter this time — or maybe I’ll just let myself spiral again into some beautiful nerd chaos. Stay tuned!

Don’t hesitate to comment, share, and most importantly, code!  
I wish you an excellent day and lots of success in your trading projects!  
La Bise et à très vite! ✌️